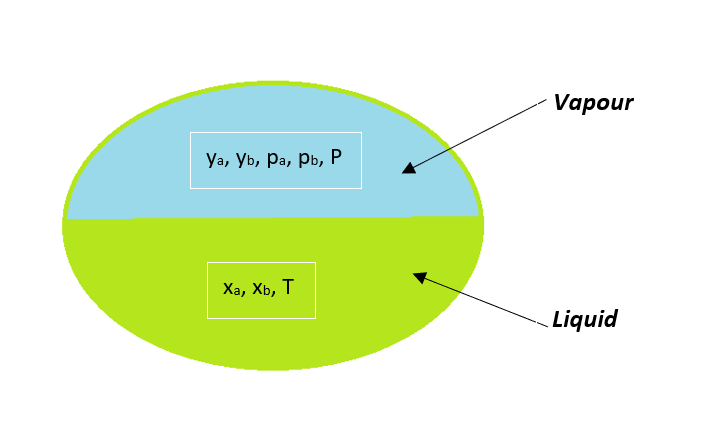
In process calculations of vapour-liquid equilibrium system there are two phases. One is vapour phase and second is liquid phase and this system can be multi-components. So, to carry out the process calculation of the unit operations involving vapour-liquid phases, we need to understand the distribution of these components between the phases. Moreover, the design and selection of an appropriate equipment depends on the vapour-liquid equilibrium behavior of that system. This behavior can be ideal or non-ideal such as azeotropic liquid mixtures.
So, first let us understand the phase rule for vapour-liquid equilibrium system.
Table of Contents
Phase Rule at Equilibrium
So, applying phase rule on a system at equilibrium we can find out number of parameters, which we can change without disturbing the system equilibrium. Let us assume, there is a vapour-liquid system which is at equilibrium. And, this system contains K numbers of components. So, if we take N as number of independent parameters (i.e., which we can change without disturbing the system equilibrium). Then applying phase rule on this system, we get following relationship:
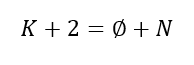
Where, ∅ is the number of phases in the system at equilibrium state.
Therefore, according to phase rule, for a vapour-liquid system with K components we get,
N = K + 2 – ∅= K +2 – 2 = K
In other words, it means the numbers of parameters which we can change without disturbing the equilibrium state of the that system is equal to the number of components K. So, for a binary system N = 2, hence we can consider below parameter combinations, which can be changed independently.
system pressure P – composition x; composition x – system temperature T; mole fraction x – y of low boiling component; composition x – H (enthalpy at constant pressure).
Next, we will discuss some basic terminologies which we use in vapour-liquid equilibrium calculations.
The Relative Volatility
In a liquid mixture, there will be one most volatile component, which has highest vapour pressure at given system temperature. Moreover, this component has lowest boiling point among other mixture components. While, the components which has highest boiling point in the mixture is a less volatile component. And, has lowest vapour pressure at the given system temperature.
Let us denote the relative volatility of the mixture by α. So, we can estimate the relative volatility by the ratio of vapour pressure of pure components A & B at the same temperature. Where, component A is more volatile and B is less volatile.
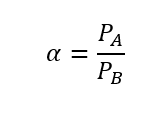
Where, PA and PB are the vapour pressure of pure individual components at the same temperature.
In case of a multicomponent system A – B – C – D having boiling points is ascending order, the relative volatility we can determine as follows:
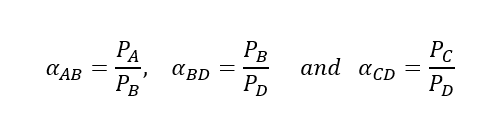
So, we can estimate the relative volatility of the component mixture based on vapour pressure of pure components at same temperature. However, there are many situations where when we don’t have relations between the vapour pressure and temperature. In that situation, we can use below equation to calculate the relative volatility.
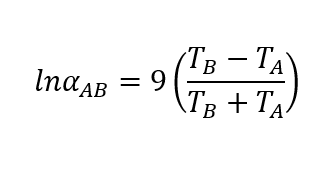
Where, TA and TB are the component boiling points in Kelvin.
Further, we can divide vapor-liquid equilibrium system in two categories. First is ideal system, while second is non-ideal system.
Ideal Vapour-Liquid Equilibrium System
For an ideal vapour-liquid system relative volatility remains constant in the component’s boiling point range. This boiling point range start from the boiling point of most volatile component to the least volatile component. Moreover, for such systems Raoult’s law and ideal gas law is valid. And, the partial pressure of the component A (which is most volatile) we can estimate using following equation:
pa = xa*PA Eq. 01
Where, pa is partial pressure of component A above liquid mixture, xa is the molar fraction of component A in the liquid mixture and PA is the vapour pressure of the pure component A at system temperature.
According to Dalton’s law, at equilibrium state molar concentration of component A in vapour space ya will be as below:
ya = pa/P Eq. 02
By eliminating partial pressure pa of component A, between equation 1 and 2 we get Raoult’s law as below,
ya = xa*PA/P Eq. 03
For a two-component system we can write below relationship between partial pressures and total pressure,
P = pa + pb Eq. 04
Using equation 1 and xb = 1 – xa, we can write below equation,
P = pa + pb= xa*PA + (1 – xa)*PB Eq. 05
Substituting the value of P from equation 5 to equation 3 we get,
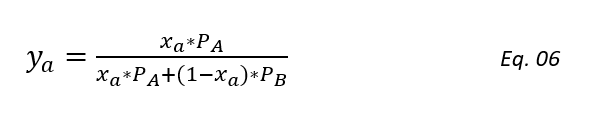
Dividing above equation by PB and substituting α = PA/PB, we get,

Above equation can be rearrange to get the below relationship between the component’s composition at equilibrium state,
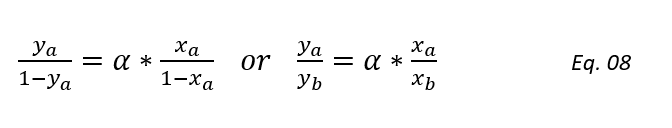
Above equation we can use to draw equilibrium distribution curve, which is the basis for distillation column design calculations.
T-x-y, P-x-y and x-y Diagram for Ideal Two Component System
Below are the T-x-y, P-x-y and x-y diagrams for benzene-toluene system at equilibrium condition, which in an ideal system.
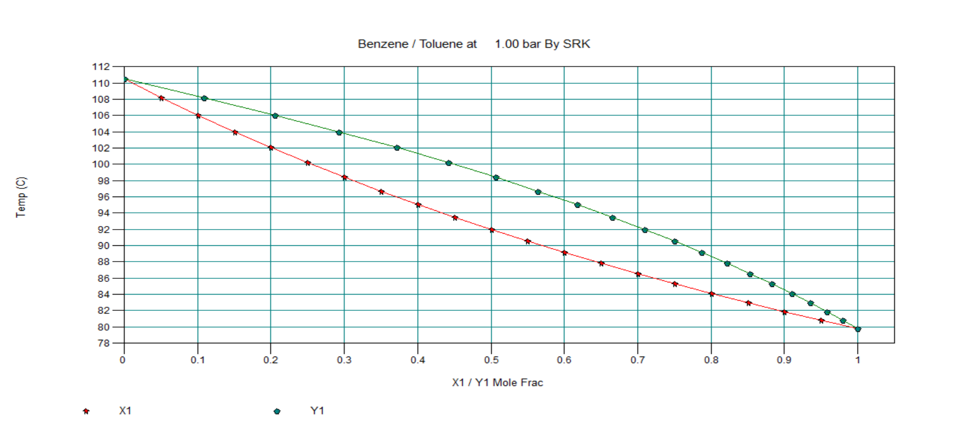
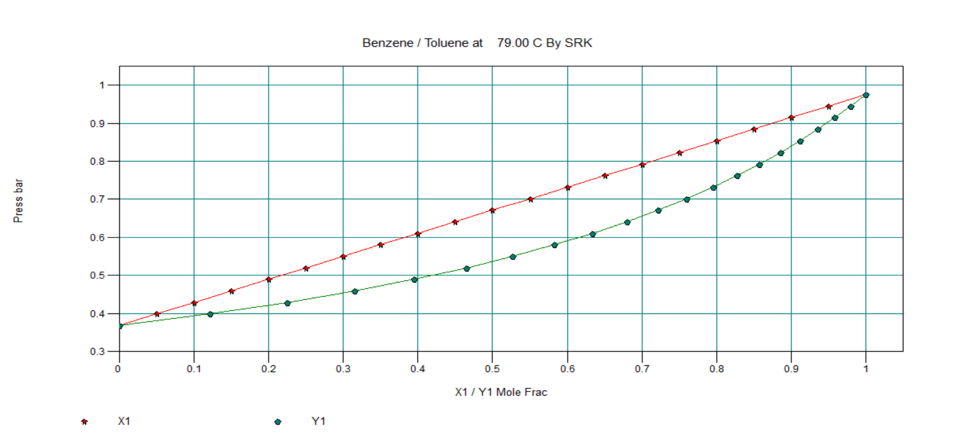
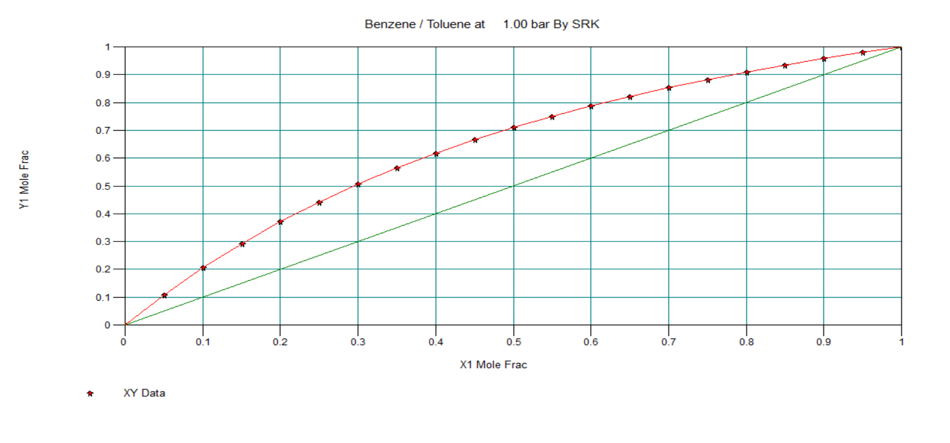
In next section, we will discuss about nonideal vapour-liquid equilibrium systems.
Nonideal Vapour-Liquid Equilibrium Systems
We can estimate the properties of mixtures of ideal gases and ideal liquids based on the properties of the pure component mixtures. However, for most of the vapour-liquid equilibrium, ideal system models are not adequate. So, for such systems the Raoult’s law, which is applicable for ideal system, can provide a reference to compare the behaviour of nonideal system with ideal system.
In nonideal vapour-liquid system, mixture’s relative volatility does not remain constant. And, for the systems when relative volatility passes through a value equal to unity is an Azeotropic Systems. In chemical process industries most of the liquid mixtures are nonideal.
Therefore, when designing a distillation column for such systems, deviation from the ideal system is accounted by the activity coefficient. This activity coefficient characterizes the activity of molecules in the mixture and molecular interactions. We can determine the activity coefficient ϒ for components A and B as below. In below equation at low pressures (i.e., up to 1.0 bar) we are considering molecular interaction in vapour phase is not significant. And, the Poynting factor which represents the nonideality of vapour phase is equal to unity (φ = 1.0).
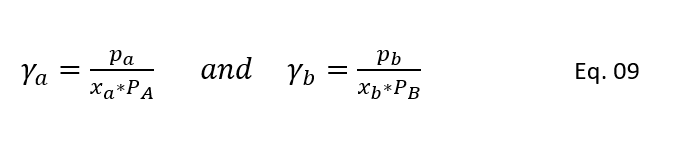
So, for an ideal system ϒa = ϒb = 1, while for a nonideal system the value of activity coefficient can be less then or greater than unity. This value depends on the magnitude of molecular attraction. Also, above equation-9, we know as modified Raoult’s law which accommodate the nonideality of the mixtures in liquid phase.
Using modified Raoult’s law, we can estimate the equilibrium distribution of components in nonideal systems. For this we need the activity coefficient of the components involved. And, we can estimate them by using equations suggested by van Laar or Redlich, Kister and Turnquist and derived on the basis of Gibbs – Duhem’s equation.
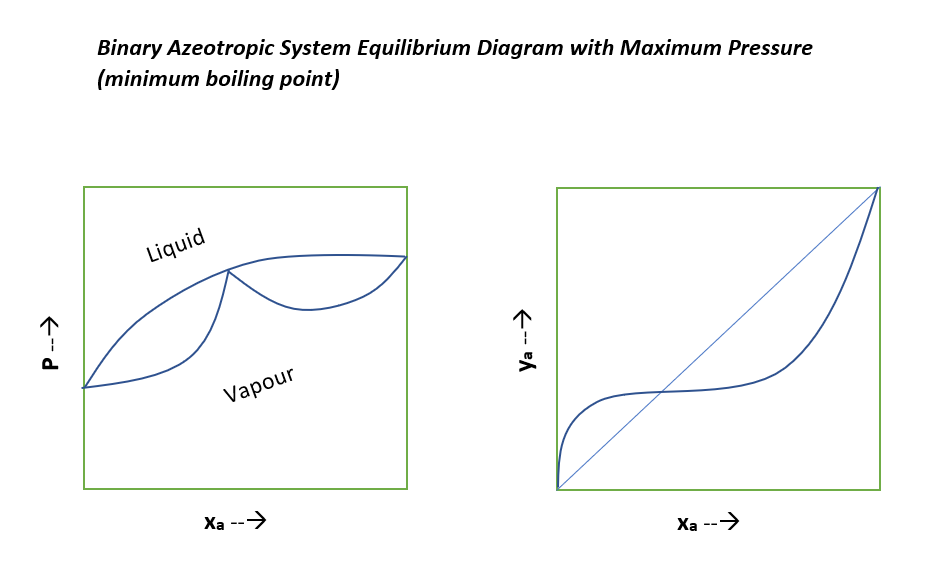
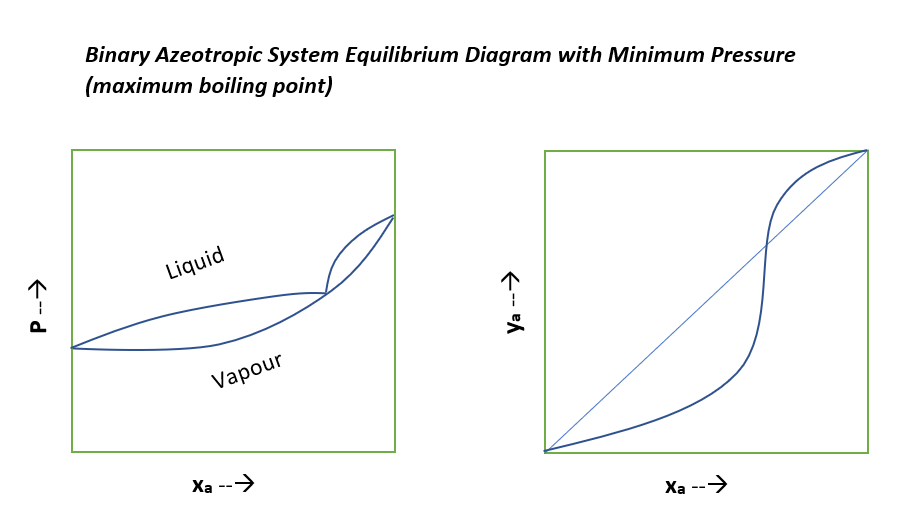
Typical Equilibrium Diagrams for Nonideal Binary System
Below are the equilibrium diagrams we can refer to understand, where relative volatility of the mixture not remain constant.
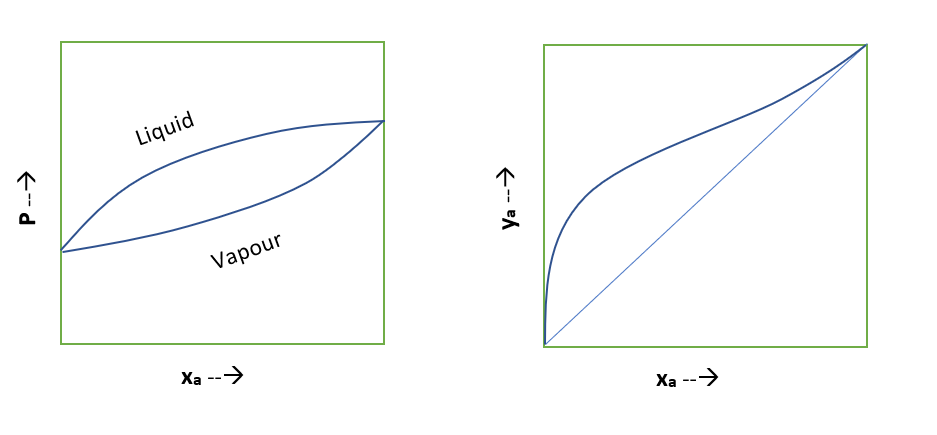
For the special cases when relative volatility of nonideal system is equal to unity, the separation of this liquid mixture is not possible beyond this composition by simple distillation methods. This type of nonideal system is known as azeotropic system. To separate these azeotropic mixture we use special distillation methods such as azeotropic distillation, extractive distillation, pressure swing distillation and molecular sieves.
These azeotropes can be minimum boiling or maximum boiling in nature. And, graphical representation for these is as below for your reference.
Conclusion
In this article we tried to understand about vapour-liquid equilibrium system. We discussed about ideal and nonideal system and derived the relationship between vapour and liquid molar compositions at phase equilibrium condition. We can use these relationships to generate vapour-liquid concentration distribution at equilibrium state.
During calculating vapour-liquid equilibrium we need to pay great attention on estimating the liquid phase activity coefficient. Because, at low pressure and far from critical conditions the density of vapour phase is relatively small in comparison with the liquid phase. Therefore, interaction between molecules is not significant in vapour phase. On the basis of this assumption, we can consider that, system nonideal behaviour is because of nonideality present in the liquid phase only.
This way we can avoid the considerable calculation for vapour phase nonideality. Moreover, when vapour phase follows ideal behaviour, the fugacity is equal to the partial of a given mixture component.
Thanks for reading.
