Background
As a process engineers many time we are required to prepare a mathematical model for non-reacting liquid tank or vessel having various shape (cylindrical, conical, wedge shaped, etc.). So, we are going to develop the same, let’s begun with a vertical cylindrical vessel shown in below figure. Consider following parameters for this vessel
- Input constant feed rate qf (m3/h)
- Output empties through a pump at constant rate q (m3/h)
- The diameter of vessel is D (m) and cross-sectional area A=πD2/4 (m2)
- liquid height in vessel is h (m) is the function of t
- liquid density is ρ (kg/m3)
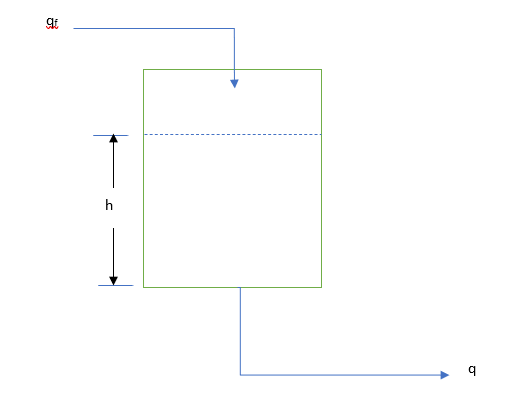
The conservation of mass for above system at time t(h) is as below
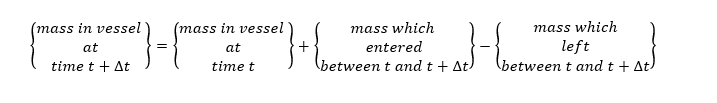
Various terms in above in above equation are as below
Mass of liquid in vessel at time t+∆t = ρ*A*h(t+∆t)
Inflow of mass vessel at any time t = qf =ρ*A*h(t) here h(t) is liquid height in vessel at time t (h)
Mass in vessel between t and t+∆t = ρ*qf*∆t
Outflow of mass from vessel between t and t+∆t = ρ*q*∆t
So, putting above all terms in mass balance equation we get
ρ*A*h(t+∆t) = ρ*A*h(t) + ρ*qf*∆t – ρ*q*∆t
Divide above equation by ρ*A to get
h(t+∆t) = h(t) + (1/A)*(qf – q)*∆t
h(t+∆t) – h(t) = (1/A)*(qf – q)*∆t
[h(t+∆t) – h(t)]/∆t = (1/A)*(qf – q)
When limit →0 the left hand side is the derivative, dh/dt and (qf – q) is constant value here evaluated at time t(h). Hence, we can write
(dh/dt) = (1/A)* (qf – q)
[d(A*h)/dt] = qf – q since V = A*h
(dV/dt) = qf – q
Mathematical Model for Wedge-Shaped Tank
Above equation is basic model equation for the system where inlet and outlet flow rates are constant. This model equation is helpful to find the liquid height at any time t(h). Now we apply this model equation on a wedge-shaped tank as shown in below figure
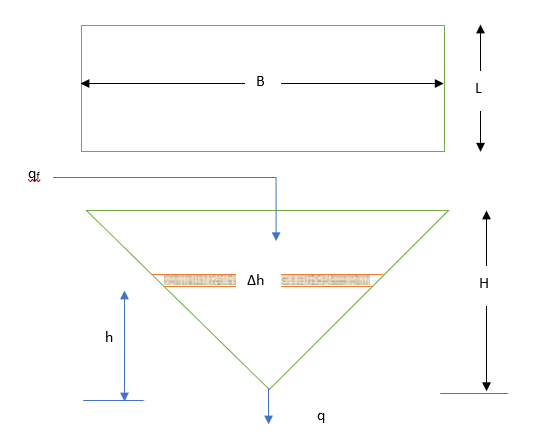
At any time, t(h) and height h(m) consider an element of ∆h having width b(m) and length (L). The volume dV will be as below
dV = dh*b*L (from geometric symmetry (b/B) = (h/H) →b = (B*h/H))
dV = (B*L/H)*h*dh
V(t) = (B*L/H)*(h2/2) = [(B*L)/(2*H)]*h2
So, substituting this in our model equation (dV/dt) = qf – q, we get below
(dh2/dt) = [(2*H)/(B*L)]*(qf – q)
For the simple case when inlet and outlet flow rates are constants we can integrate above equation as below
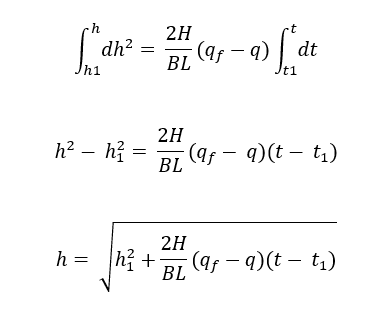
Here, h1 is the liquid height at time t1.
Conclusion
Above model equation are helpful to understand the system behavior of non-reacting liquid tank with changing the different values of qf and q. Moreover, this model is helpful in control system design for liquid level in the tank.
Thanks for reading, looking forward for your valuable comments and inputs.

