In Chemical Process Industries, we transfer gas or liquids from one point to another point. And, for this purpose we use pumps, fans, compressors and pipe lines accordingly. As a process engineer, we need to do the process calculations to estimate the power requirement, flow rates and pressure drop through this piping network. So, to do these calculations, in this article we will discuss energy balance at steady state for control volume system.
To start with let us consider a control volume system as shown below.
Table of Contents
Control Volume System
In below figure we consider a close volume system. In this system fluid enters at point ‘a’ and leaves at point ‘b’. Also, ‘Ws’ is the work done by system in J/s and ‘Q’ is J/s heat absorbed from surroundings.
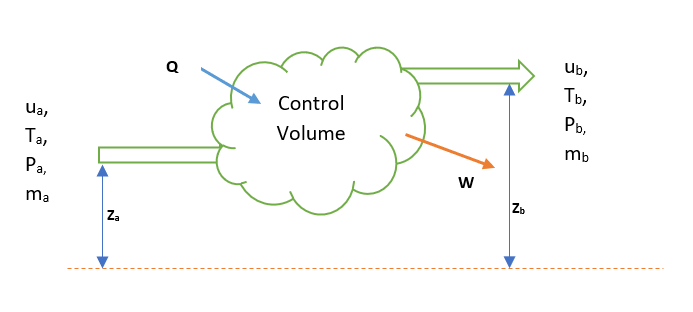
So, total energy balance for above system at steady, between the point ‘a’ and ‘b’ will be as below. This we can write using the first law of thermodynamics for control volume system (between point ‘a’ and ‘b’).
(Rate of Accumulation of Energy) = (Rate of Energy inflow) – (Rate of Energy outflow)
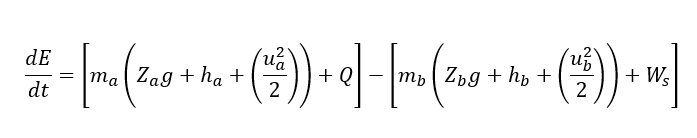
In our plants devices such as pumps, compressors, turbines, fans etc. operates at steady state conditions except the time of start up and shut down. These unsteady state conditions are very small duration in comparison with the steady state operation time. So, it is more logical to do the analysis of steady flow to evaluate the performance and design of these devices.
Therefore, we can consider dE/dt = 0, ma = mb = m. Hence, we can rewrite above equation as below:
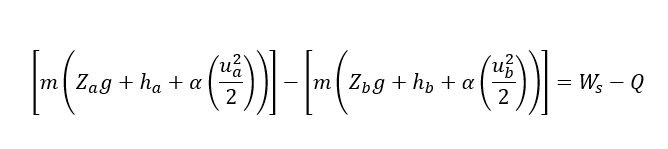
In above equation ‘Ws’ is the energy added to system (in form of work) in J/s and ‘Q’ is J/s heat absorbed from surroundings. Here, ‘P’ is pressure (pascal), ‘Z’ is height from ground level (m), ‘v’ is volume (m3), ‘u’ is fluid velocity (m/s) & ‘g’ = 9.81 m/s2.
Also, ‘α’ is the correction factor in kinetic energy term. For a uniform velocity profile and turbulent flow, α = 1. For laminar flow in a circular pipe with a parabolic velocity profile, α = 2.
Applications of Steady State Flow Processes
- For Compressors & Turbines we can ignore kinetic energy and potential energy terms without appreciable error. Moreover, assuming these devices operating under adiabatic conditions. The above-mentioned control volume steady state energy balance reduces to as below: (i.e., KE = PE = Q = 0)
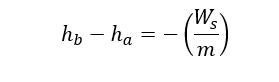
Note: Ws is positive for turbine & negative for a compressor.
- A nozzle as shown below, we use to increase the flow velocity for the fluid.

So, for this case energy balance for control volume gives:
ub2 – ua2 = 2*(ha – hb) = 2*∆h = 2*Cp*(Ta – Tb)
For the case when inlet fluid velocity is ua << ub, we can rewrite above expression as below:
ub = [2*Cp*(Ta – Tb)]1/2
Mechanical Energy Balance, Bernoulli Equation
In below PFD you can see liquid from a tank is going into the pump suction. From the pump discharge this fluid passes through a heater and then enter into a reactor.
The mechanical energy balance includes kinetic energy, static energy and potential energy. We can write Bernoulli equation between point ‘a’ and ‘b’ without considering friction term as below:
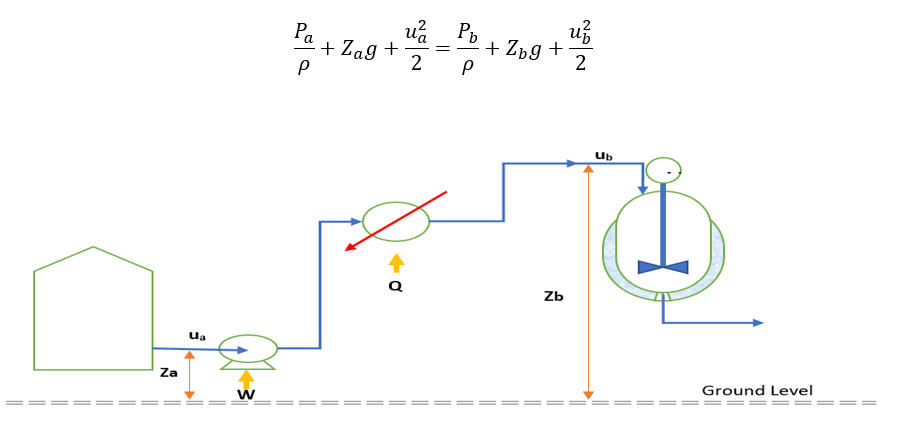
To make above equation more useful for a pumping system as shown in above figure. We require to make two corrections. First is correction for kinetic energy term, which is because of variation in velocity because of position in boundary layer. The second, which is more important is correction for friction losses due to fluid flow and boundary layer formation.
So, below is the corrected Bernoulli equation for incompressible fluids: –
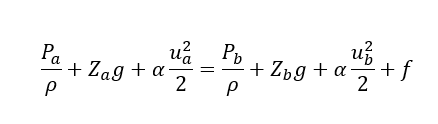
In above equation ‘f’ is the mechanical loss at all points between point ‘a’ & ‘b’ in above figure. Also, in a piping network we use a pump to overcome this friction loss ‘f’. Hence, we can correct above equation for pump work as below:
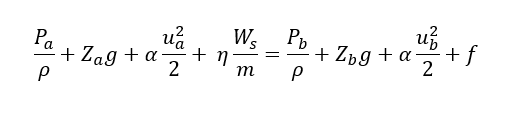
Now, let us consider one example to see the utility of above equation for the flow of incompressible fluids.
Example for Pumping of DM Water from Tank to Reactor
Let us refer to above PFD for pumping system, pump draws DM Water from the tank through 100NB, Sch-20, SS304 pipeline. The discharge pipeline size is 80NB, Sch-20, SS304. The efficiency of pump is 70% and elevation difference between tank level and reactor inlet is 12 meters. The reactor is operating at atmospheric pressure. Total friction losses between point ‘a’ & ‘b’ is 15 meters.
Average velocity through pump pipe at reactor inlet is 2.5 m/s. Calculate power requirement for the pump & motor size.
To estimate the power requirement, we will use the below equation:
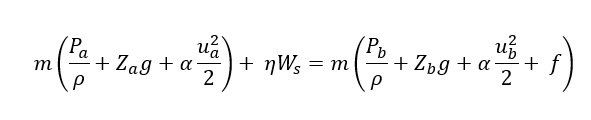
Various available information in above equation are as follows:
- Pa & Pb are equal to atmospheric pressure (i.e., will cancel out both side)
- (Zb – Za) = 12 meters and g = 9.81 m/s2
- Discharge pipe ID, Db = 84.69mm & Suction pipe ID, Da = 110.08mm
- Pump efficiency, η = 70% and f = 15*9.81 (m/s)2
- Flow is turbulent so, α = 1.0
Discharge velocity, ub = 2.5 m/s hence ua = (Db/Da)2*ub = (84.69/110.08)2*2.5 = 1.48 m/s
Flow area of discharge pipe = pi()*(84.69/1000)2/4 = 0.005633 m2
Hence mass flow rate from the pipe line, m = 0.005633*2.5*1000 = 14.083 kg/s
After putting all values in above equation, we get:
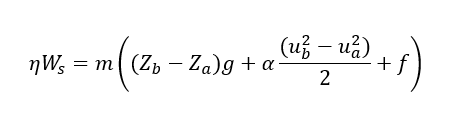
ηWs = 14.083*(12*9.81 + (2.52 – 1.482)/2 + 15*9.81) = 3737.5 kg-m2/s3
Ws = 3737.5/(70/100) = 5339 Watt
Considering motor efficiency 95% required motor rating will be, Em = Ws/0.95 = 5339/(0.95*1000) = 5.62 kW
Conclusion
So, in this article first we discussed total energy balance for a control volume system. And, subsequently we saw the application for turbine/compressor and nozzle. After this we worked out with mechanical energy balance or Bernoulli equation for a liquid pump and piping network. Also, we took one example for pumping DM water from the tank to reactor and estimated the power requirement for the pump & motor.
Thanks for your reading.
