Model Equation for Agitated Continuous Reactor

In chemical engineering, model equation enable us to understand the behavior of the process. Therefore, using mathematical models we can run the process virtually and get optimum operating process parameters. Afterwards, we can use these optimized parameters for real life process.

System Description

We have an agitated reactor having volume V, in which two liquid streams are incoming. Both liquid streams are two different chemicals A and B. When these two chemicals contact with each other into the reactor, they react and forms a new chemical D. The volumetric flow rates of chemical A and B are q_Af and q_Bf respectively. The concentration of chemical A & B in their feed are C_Af and C_Bf. The reactor is well mixed. Exit stream volumetric flow rate is q and concentration of various chemicals are C_A, C_B and C_D. The schematic figure of system is as below

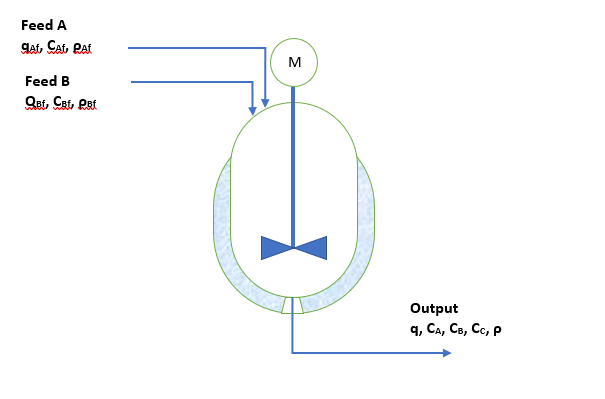
Apply the law of mass conservation between a time span t₁ and t₂ which is very small-time interval (i.e., t₂-t₁=∆t)

Total Mass Balance

So, we can write the total mass balance for above control volume system as below

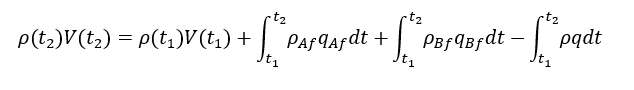
Integration of above equation will give

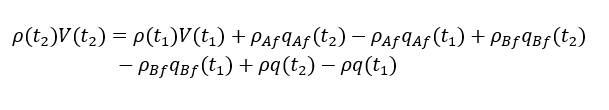
considering t₁ = t and t₂ = t + ∆t, assuming ρ & q constant and t₂-t₁=∆t →0

Component Mass Balance

Mass balance for Chemical species A will be as below for the control volume V,

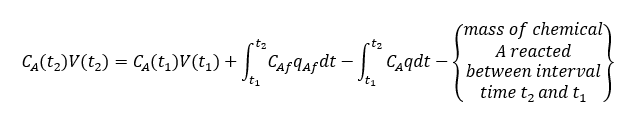
For our system let us assume the reaction between A and B is as below

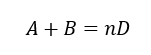
Rate of consumption for chemical A in reaction = r_AV

Amount of chemical A converted because of reaction between time t2 and t1 = r_AVdt

So, component mass balance for species A will be, putting consumption term in above equation

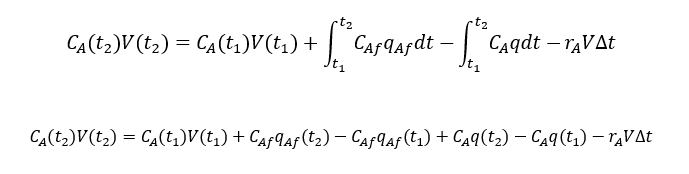
considering t₁ = t and t₂ = t + ∆t, assuming ρ & q constant and t₂-t₁=∆t →0

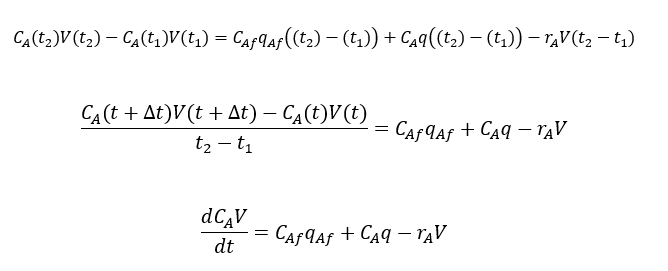
Similarly, we can write component balance for chemical B and D also

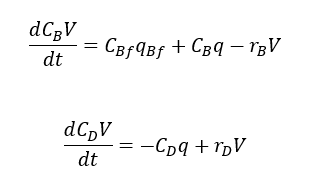
From reaction we understand that, one mol of A reacts with one mole of B to form n mols of D. So, we can write the relationship between rate of reactions

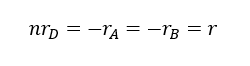
Then component balance will become as below

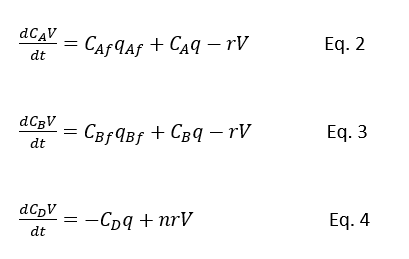
Equations are Eq.1 to Eq.4 are the basic model equations for a well-mixed agitated reactor in which the liquid phase reaction between A and B to form D is taking place.

Model for Batch Reactor

For modeling let us take following assumptions

Densities of all streams are equal (i.e., ρ = ρ_Af = ρ_Bf )

since this is a batch reactor, so there is no in or out flow from this (q_Af = q_Bf = q = 0) and volume V is constant, Equation for 2 to 4 will reduce to

Equation from Eq.5 to Eq.7 are basic model equation for batch reactor system.

If initial total concentration of A and B in reactor is C_A0 and C_B0 respectively than, M = C_A0 + C_B0 . Hence C_B = (M – C_A)

For our system let us assume the reaction between A and B is as below

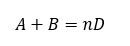
Assume this is elementary reaction than rate of reaction will as below

r = kC_AC_B

The Eq.5 will be reduced as below

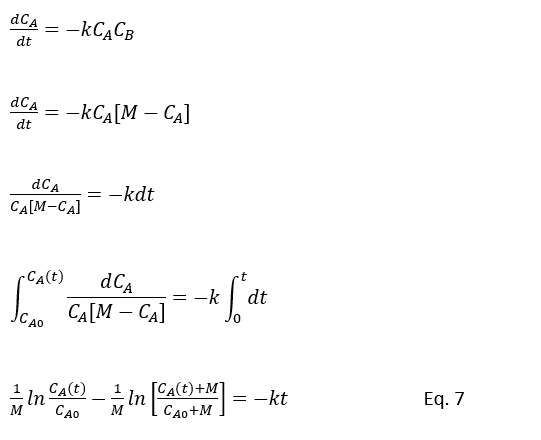
Eq.7 will reduce for C_A in a batch reactor with second order rection A + B → nD, for equal (M=0) starting concentration

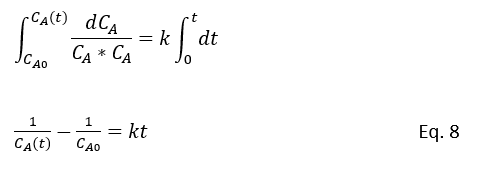
Sample Problem

The hydrolysis of acetic anhydride in excess water to form acetic acid (CH₃CO)₂O + H₂O → 2CH₃COOH and the rate of reaction at 15 ⁰C can be expressed as r = kC_A, k=0.0567 min^-1. This reaction study takes place in a batch reactor and initial concentration C_A0 = 100 lb of acetic anhydride. So the time taken to convert 90 lb of anhydride can be estimated by model equation Eq. 5.

C_A0 = 100 lb, C_A = 90 lb and k = 0.0567 min^-1  

Reference: Introduction to Chemical Engineering Analysis, T.W.E. Russell & M.M. Denn.