Background
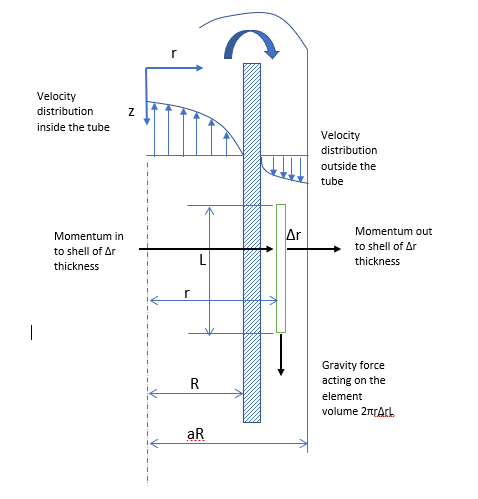
In real life as a process engineer we face situations where we need to calculate the velocity distribution and film thickness of falling film outside of a circular tube. For example, falling film evaporator, falling film gas absorption, where a viscous fluid flows upwards through a small circular tube and after that it overflow outside of tube as shown in below figure.
For the steady-state flow, the momentum balance equation can be written as
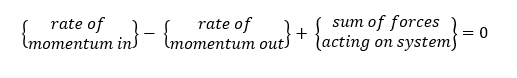
We consider a shell of thickness of ∆r and length L in falling liquid film at the radius r. In this case end effects are neglected and fluid is in-compressible.
The various contributions to momentum balance in the z-direction are as below

Putting all above values in momentum balance equation we will get as below
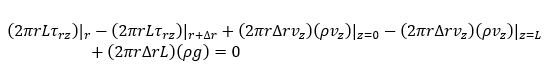
In above equation 3rd and 4th term will be cancelled out, because fluid is incompressible and velocity is z-direction is constant. So, we can rewrite the above equation as
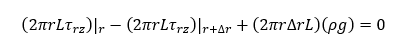
Divide the above equation by 2πL∆r and rearrange we will get
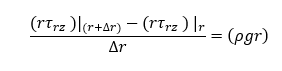
Take the limit as ∆r → 0; this gives
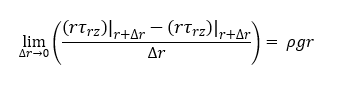
The expression on the left side is the definition of the first order derivative. Hence, we can write this as below
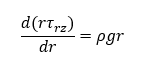
Integration of above equation will give as follows
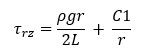
To estimate the integration constant, we apply the following boundary condition at gas-fluid interface. At r = aR, the sheer stress τrz = 0, hence we can solve for C1
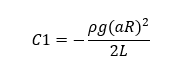
Substituting value of C1, we can write the equation for momentum flux distribution
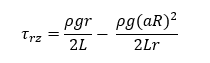
The Newton’s law of viscosity is given by
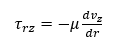
Replacing the value of τrz in momentum flux distribution equation we get
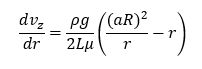
Integration of above equation will give
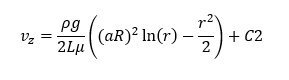
To estimate the value of integration coefficient of C2 we use boundary condition at r = R, vz = 0,
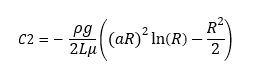
Replacing value of C2 in above equation we will get velocity distribution equation for the system

The volume rate flow in the thin film can be given by Q = Flow are of film* Velocity
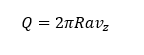
References
TRANSPORT PHENOMENA, R. Byron Bird, Warren E. Stewart and Edwin N. Lightfoot, Chapter 2, Problem 2.G2.

